The Inexistent Pyramid & A Generalization of BANACH-MAZUR Lemma

First, let me give you some context. There is a certain theorem saying that the complex numbers are algebraically closed. That is known as the "Fundamental Theorem of Algebra". Think about the real numbers: $p(x) = x^2 + 1$, with $x \in \mathbb{R}$ has roots that lie outside $\mathbb{R}$. What the theorem is telling us is that any polynomial $p(x) = a_n x^n + a_{n-1} x^{n-1} + \ldots + a_1 x + a_0$, with $a_i \in \mathbb{C}$ has at least one complex root.

The theorem has a long and rich history, with mathematicians such as Euler and D'Alembert pioneering attempts at proving the theorem, and later proofs by Argand and Gauss. The exhibition below gives a much simpler proof based mainly on basic geometrical calculations, of a related Lemmma which, with a page worth of (not so hard) reasoning, results in the Fundamental Theorem of Algebra. If you want to check alternative versions of proof and a the complete version from the Gelfand-Mazur Lemma to the Fundamental Theorem of Algebra, reach out to us at anna@hisolver.com; Now let's get to it ✨

In this brief exposition we will enunciate a theorem and develop a sketch of one proof of it, which is very fertile generalization of the famous, celebrated and fundamental Gelfand-Mazur Lemma in the theory of normed algebra.

We count on, for reasons of brevity, the audience's knowledge of the context in which this Lemma sits: the theory of unitary banach C-algebras (here C denotes the complex number field). This lemma states:

"If $A$ is a unitary Banach C-algebra, for any element $a$ of $A$, there exists a complex number $\lambda$ such that $a - \lambda$ is non-invertible in $A$" 

Here $\lambda$ denotes its 'partner' in A, which is $\lambda \cdot 1$, where $1$ is the unit of $A$, in a harmless abuse of notation.

The generalization mentioned above is the following:

"If A is a R-algebra and E is a R-vectorial subspace of A, for which all elements commute, and any nonzero element of E is invertible in the completion $\hat{A}$ of A, then E has at most two independent vectors."

Here, R denotes the real number field.

In following sketch of the proof of this result, the principal character is a pyramid. By the way, it is informative to mention that we have also two more proofs alternative to the one which will follow below, working on the same pyramid, but also another which is inspired by Euler's style, and developing an argument originally formulated by D'Alembert in terms of the differential form $x^ {-1} dx$ on E \ {0}, with values in $\hat{A}$, and one possible primitive L for it. This is possible under the assumption that E has more than two independent vectors, in which case in the space F generated by three independent vectors, the complement of zero, F \ {0}, being simply connected guarantees the existence of L in it, as a consequence of the commutativity of E.

Following D'Alembert, we consider dL(-x) = (-x)^{-1} (-dx) = x^ {-1}dx = dL(x), and differently of D'Alembert, we observe that d( L(x) - L(-x) ) = 0, hence L(x) - L(-x) is constant, since F \ {0} is connected. Also, observing that changing x to -x, this difference don't change, and on the other hand, changes to -( L(x) - L(-x) ). Hence, the constant is zero. Conclusion, L(x) = L(-x).

To conclude the argument, in Euler's style, we get $d(x e^{-L(x)} ) = 0$, which implies that $x e^{-L(x)}$ is constant. Again, changing x to -x we get $x e^{ - L(x) } = (-x) e^{ -L(-x) }$, and using that L(x) = L(-x), we can cancel the exponentials and obtain x = -x, that is x = 0. Contradiction.

After this brief digression, we go to the proof on the pyramid.

Again, by way of contradiction, assume that E has three independent vectors, let's say u, v, w. Now consider the pyramid with the parallelogram generated by -u, -v, u, v as its base, and summit (top vertex) w. 

In the faces of this pyramid, consider a web formed by two sets of transversal paths, one connecting -u to u, by two segments, one from -u to z and another from z to u, for each z of a finite set G of points on the path from -v to v constituted by two segments, one from -v to w, and the other from w to v. This finite set will be specified under a convenient condition to develop the proof. Below you can dynamically visualize the paths on the faces of the pyramid:

And a picture of the paths.

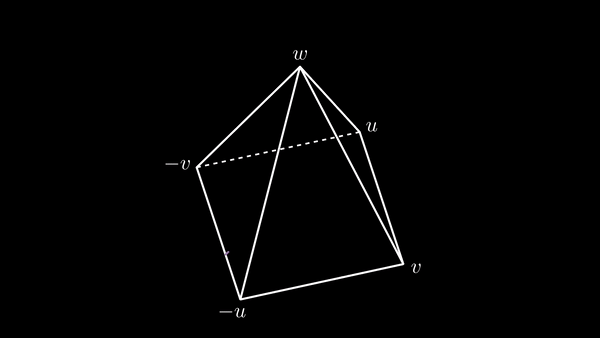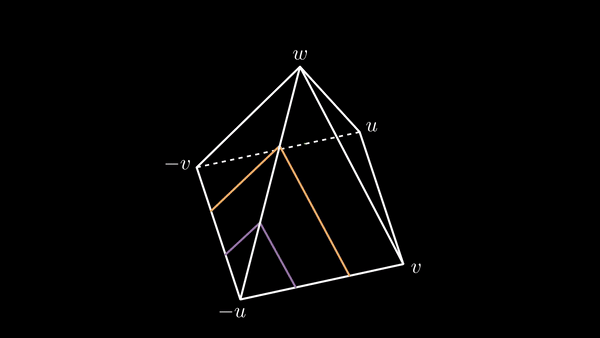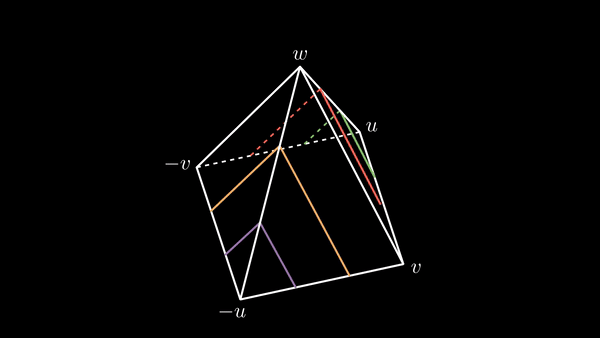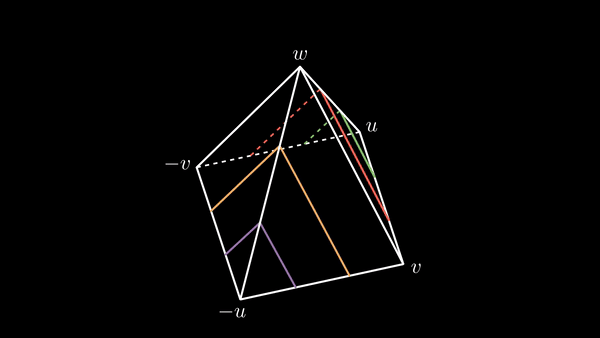
In the union of the two segments, one from -u to v and the other from v to u, we fix another finite set H of points, also to be specified later, which has the same number of points in the two segments, the one from -u to v, the other from v to u. We add to this set the opposite of each of its points, which lies in the opposite sides of the base of the pyramid, that is the union of the two segments, one from -u to -v, and the other from -v to u.

We consider also a finite set J of points in the union of the two segments, one from -u to w, and the other from w to u, to be specified later under  a convenient condition to develop the proof, with the same number of points as H, in each one of the corresponding pair of segments, the one from -u to v with the other from w to u.

After this we connect each point h of H on the segment -u to v to the corresponding point in the segment -u to -v, sequentially, by means of the union of two segments, one from h to the corresponding point of J in the segment -u to w, and the other from this point of J to the mentioned point of the segment -u to -v.

Analogously, we do similar connections, sequentially, from each point of the segment v to u, to the corresponding point of the segment -v to u, also passing by the corresponding point of J in the segment from w to u. Next you can dynamically visualize the paths:

And the still visualization of the paths:

This web produces a set of quadrilaterals determined by each of two pairs of adjacents and transversal lines, with the exception of the triangles with two sides in adjacent lines in the pencil of lines from -u to u, some of them having -u as the common vertex of these two sides, and the others having u as the common vertex of these two sides.

We fix one orientation in each of these quadrilaterals and triangles, coherently in such a manner that quadrilaterals or triangles which have common sides, the induced orientation in these sides are opposite.

The pyramid illustrations above have some distortions with respect to perspective to facilitate the view of the lines.

Now we invoke one crucial auxiliary piece of the argument, an analytical one, a local inverse of the square function Q on the algebra $\hat{A}$. This local inverse, which will be defined in some ball B_1 contained in $\hat{A}$ around the unit element, can be obtained by direct application of one version of the Inverse Function Theorem, for example, observing that the square function satisfies the condition of strong differentiability at the unit element. As a consequence of the process of determining R, the image of B_1 by R can be assumed to be contained in a ball B in which Q is injective.

Let's denote this local inverse by R, which satisfies Q(R(y)) = R(y)^2 = y, for y in the domain B_1 of R, and R(1) = 1.

We need also fix some ball B_2 around the unit element, in such a way that the product of any four elements of B_2 belongs to B_1, as the product of any four elements of the image of B_2 by R belongs to the mentioned ball B in which Q is injective. In particular, B_2 is contained in B_1, since the unit element is contained in B_2, and for each element y of B_2, $y \cdot 1 \cdot 1 \cdot 1 = y$. Also for any four commuting elements $a, b, c, d$ of B_2, $R(a \cdot b \cdot c \cdot d) = R(a) \cdot R(b) \cdot R(c) \cdot R(d)$. This can be obtained from the commutativity of the values of R on a, b, c, d, as a consequence of the commutativity of a, b, c, d, and the fact that the values of R are determined by a limit of an iterative process beginning with 1, and if the values of R are considered on elements of B_1 which commute, they will also commute because in each step of the iterative process they will commute, and the values of R are limits of these commuting elements of the iterative process. We must also add the observation that the value of Q on the two sides of the above equality involving R that we want to prove are equal because the factors of the product on the right side commute, and so the square of this product is the product of the squares of the values of R is $a \cdot b \cdot c \cdot d$, as the square of the left side, and finally by the reason that the two sides are elements of B where Q is injective.

To reach the final computation on the pyramid involving the quadrilaterals and triangles described above, we will need one more restriction, which is the proximity of neighboring points in G, H, and J in such a way that the product $y \cdot z^{-1}$ belongs to B_2 for any two elements y, z of the same quadrilateral or triangle.

First, for any quadrilateral, with vertices f, g, h, k, positioned in a cyclic sequence following the fixed orientation, taking $a = g \cdot f^{-1}$, $b = h \cdot g^{-1}$, $c = k \cdot h^{-1}$, $d = f \cdot k^{-1}$, and we observe that $a \cdot b \cdot c \cdot d = 1$, because f, g, h, and k commute. Now $1 = R(1) = R(a \cdot b \cdot c \cdot d) = R(a) \cdot R(b) \cdot R(c) \cdot R(d)$. Similarly, for the triangles with vertices p, q, r, positioned in a cyclic sequence following the fixed orientation, taking $a' = q \cdot p^{-1}$, $b' = r \cdot q^{-1}$, $c' = p \cdot r^{-1}$, and we observe that $a' \cdot b' \cdot c' = 1$, because p, q and r commute. Analogously, $1 = R(1) = R(a' \cdot b' \cdot c') = R(a') \cdot R(b') \cdot R(c')$.

In the next step we consider the product of all products $R(a) \cdot R(b) \cdot R(c) \cdot R(d)$ corresponding to the quadrilaterals and $R(a') \cdot R(b') \cdot R(c')$ corresponding to the triangles, and we observe that this product is 1, because individually each product coming from the quadrilaterals and triangles is 1.

On the other hand, each factor of the products above (coming from quadrilaterals or triangles which corresponds to successive vertices f, g which are common to neighbor quadrilaterals or triangles) cancel, with the other factor coming from the same vertices in the neighbor quadrilaterals or triangles, because $R (g \cdot f^{-1}) \cdot R(f \cdot g^{-1}) = R (g \cdot f^{-1} \cdot f \cdot g^{-1}) = R(1) = 1$.

As a result, the product of all products of four factors coming from quadrilaterals and three factors coming from triangles is equal to the products of the factors coming from vertices in the base of the pyramid.

Corresponding to each factor $z \cdot y^{-1}$ coming from neighboring vertices y, z of the segment from -u to v we have a factor $(-z) \cdot (-y)^{-1} = z \cdot y^{-1}$. Similarly, to each factor $z \cdot y^{-1}$  coming from neighboring vertices y, z of the segment from v to u, we have a factor $(-z) \cdot (-y)^{-1} = z \cdot y^{-1}$.

Considering the equality of each factor coming from neighboring vertices from the union of the two segments, one from -u to v and the other from v to u, with a corresponding factor coming from neighboring vertices from the union of the two segments, one from -u to -v and the other from -v to u, the product of all factors considered above, results in the product of the squares of the factors coming from the two segments, one from -u to v and the other from v to u.

Finally, this product of squares of the factors mentioned above results in a product of a sequence of factors constituting a telescopic product, because these squares are of the type $Q(R(z \cdot y^{-1})) = z \cdot y^{-1}$, where z is the neighboring vertex of y in the order beginning in -u and reaching u passing by v in the set H.

In this telescopic product, the first element of the sequence is -u and the last is u, and since all the intermediate elements y of the sequence between -u and u cancel with its inverse $y^{-1}$ remaining only $u \cdot (-u)^{-1} = u \cdot -(u^{-1}) = -u \cdot u^{-1} = -1$. But we already know that this product is 1.

We arrived at a contradiction $1 = -1$.

We conclude that the assumption that E has more than two independent vectors is contradictory. And then the proof is concluded ☠️